
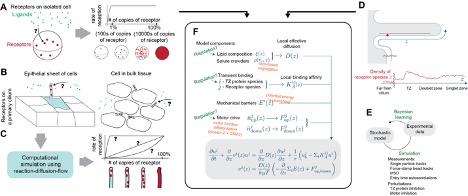
2022 Project Descriptions
Our lab uses physics to understand components inside cells. One such cellular component is the primary cilium, the “antenna” of the cell used to receive signals from other cells. It is used by human cells in many roles, including skin healing and brain structure. Defects in the cilium are connected to disease, including skin cancers and neurological conditions like schizophrenia. Mystery: New data from labs at UCI (one [Atwood Lab, Dev & Cell] that studies skin, and one [Alachkar Lab, Pharm Sci] that studies brain) show that certain cilia change length and molecular content during disease. How does that affect signaling? Since the circumstances are so different, we speculate that there is a mathematical reason. We will use a one-dimensional advection-reaction partial differential equation model to test these ideas. This model will receive inputs from (1) a high-performance computing particle-based reaction-diffusion solver, and (2) single-particle-tracking experimental data using statistical Bayesian learning algorithms.
Skin contains dendritic cells (DCs) that can be activated and migrate to skin-draining lymph nodes to initiate an adequate T cell-mediated immune response. DC migration is known to be impacted by the dermal microenvironment that contains myriad cell types including the fibroblasts. However, little is known about the signaling interactions between DCs and dermal fibroblasts that might shape immune responses. The goal of this project is to utilize our existing single-cell RNA-sequencing data to first define the transcriptional heterogeneities in skin DC and fibroblasts, and then study the potential signaling communications among different cell subsets based on ligand-receptor expression. Students will be introduced to basics in scientific literature reading and hypothesis generation, as well as single-cell data analysis pipelines such as using Seurat and CellChat.
Ultrasensitive dose responses allow biological systems to take decisions, in that these responses have either very large or very small outputs as a function of a continuously increasing input. How to create such all-or-none respones using only widely available tools from biochemistry is an important challenge when understanding signalling responses and cellular communication. We explore the question of composing multiple ultrasensitive responses as a way to increase the ultrasensitive behavior, as well as exploring a new mechanism of ultrasensitivity involving saturating functions.
Demographic models study human population dynamics by tracing individuals of different age-groups. On the other hand, epidemiological models are used to understand the spread of disease in populations of people. In this project, we will combine demographic and epidemiological models to understand disease spread in populations of individuals with a realistic age structure. We will use real-world data on the amount of contacts that people of different age groups have with each other, and identify which types of contacts (school, work, home) are the most important in the epidemic spread.
A hallmark feature of many cancers, and an enduring puzzle of biology since its discovery in the 1950’s, is a phenomenon called the Warburg Effect. Here, cancerous cells gain access to oxygen, but then shift their metabolism to aerobic glycolysis, away from (oxygen-using) oxidative phosphorylation (OXPHOS) to favor glycolysis, despite the availability of sufficient levels of oxygen. This is especially intriguing since glycolysis is much less efficient than OXPHOS in producing energy. However, it is increasingly recognized that glycolysis is not a singular choice for all cells in a tumor; OXPHOS modes of metabolism may be dominant to some cells but not others. The proposed outcome of this heterogeneity is that cooperation between these two groups of cancer cells can maximize the delivery and consumption of nutrients and minimize the environmental stresses that are imposed on a tumor. This is known as metabolic symbiosis. For example, glycolytic cells produce lactate that can be used as fuel by cells using OXPHOS. Figure 1 shows metabolism under varying oxygen concentrations.
In this project, students will develop deterministic and stochastic population-based and individual-based mathematical models to determine conditions under which metabolic symbiosis is not just a manifestation of tumor heterogeneity, but is a fundamental aspect of tumor survival. That is, students will determine conditions and parameter ranges for which tumors that display metabolic symbiosis have an enhanced fitness compared to those in which there is metabolic homogeneity. The population-based modeling will use ordinary and stochastic differential equation models while the individual-based modeling will use CompuCell 3D, which is based on the Cellular Potts approach, as the primary modeling tool. We have extensive experience using these approaches. Model predictions will be compared to results in the experimental literature.
The mathematical challenge lies in developing a model that, on the one hand, contains all the relevant biological features needed to compare with experimental data, and, on the other, is simple enough to provide insight into the underlying mechanism of spatial heterogeneity.

In collaboration with the Khodjakov Lab at the NY State Department of Health, we have 3D spatial trajectories of chromosomes during mitosis (cell division). When the chromosomes make it to anaphase, they are meant to rip apart. However, some do not, and the cell fails to undergo mitosis. The goal of this project is to investigate whether the outcome of the trajectories can be predicted from machine learning. If so, what factors determine their fate? The project will consist of data processing and programming machine learning algorithms to explore this data.
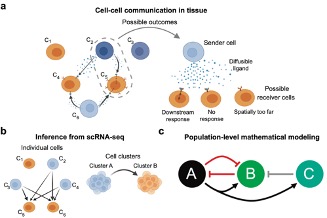
In disease or cancer, various types of cells (e.g. tumor cells and immune cells) actively “chat” with each other to influence their behaviors, through a process termed cell-cell communication (CCC). CCC plays a vital role in determining the progression of disease inflammation or tumor growth. Recently, the high resolution and throughput of single-cell RNA sequencing (scRNA-seq) has provided an unprecedented opportunity to infer large-scale CCC in biological processes. On the other hand, mechanistic mathematical modelling of CCC also facilitates the quantitative description and prediction for the long-term dynamical behavior of key cell populations.
In this project, we will integrate both machine learning and mathematical modeling approaches to dissect significant patterns of CCC and predict the outcome of CCC from scRNA-seq data. Using cutting-edge tools for CCC inference, the analysis will reveal novel communications among different cell types, as well as their downstream effects in various cell types. From this data analysis, mechanistic models will be built to predict the dynamical outcomes of such communications on cell populations, providing new insights to understand and discover the potential treatment strategy and therapy for the tumor or disease.
Many cellular functions, including certain metabolic and gene-regulatory processes, involve periodic oscillations. For example, the circadian cycle—referring to the physiological night-day cycle experienced by most organisms on earth—involves oscillating cellular concentrations of various metabolites, proteins, and genes, with a 24-hour period. Concentrations of biomolecules also tend to be “noisy”—meaning that their levels fluctuate up and down in a non-periodic manner. This project will use mathematical modeling to study the sensitivity of biomolecular oscillations to noise. We will be studying a group of models of biological oscillators using differential equations and stochastic simulations. We will study how different parameters control the onset or decay of oscillations, and determine whether these phenomena are sensitive to noise. The results may guide future strategies for engineering bacteria with non-natural cycles.
Cancer is a collection of diseases characterized by unchecked growth toward limitless expansion. Basically, it is a disease in which some of the body’s cells grow uncontrollably and spread to other parts of the body. TGF-β is prominently known to play dual roles as tumor inhibitor and tumor promoter, but the mechanism that activates the switch is still unclear. Many studies have identified the overexpression of TGF-β1 in various types of human cancer, which correlates with tumor progression. The goal of this project will be to propose a mathematical model with the purpose of studying the double-sword role of TGF-β in Cancer.
The over-arching goal of my research is to develop novel machining learning methods to decipher the fundamental principles of gene regulation and bridge the gap between genotype and phenotype in genetic disorders. Our lab focused on developing standard consortia data analysis pipelines, integrating large-scale genomics data, constructing the official ENCODE compact genome annotations for disease studies, and prioritizing noncoding regulatory elements for functional validations. Besides, I applied my knowledge of machine learning practices to regulatory genomics and developed several tools to pinpoint disease-causing network changes, cis-regulatory elements, and genetic variants in the human genome. Recently, my laboratory has placed a heavy focus on developing novel algorithms for single-cell regulatory genomics.
